Differentiable simulation for physical system identifiaction

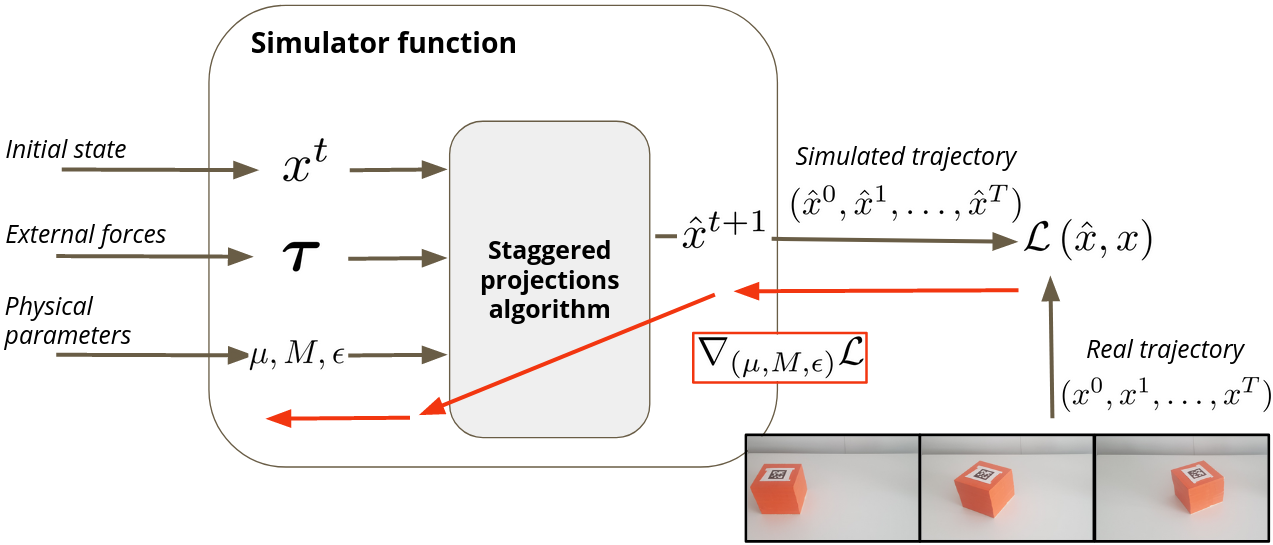
Abstract: Simulating frictional contacts remains a challenging research topic in robotics. Recently, differentiable physics emerged and has proven to be a key element in modelbased Reinforcement Learning (RL) and optimal control fields. However, most of the current formulations deploy coarse approximations of the underlying physical principles. Indeed, the classic simulators lose precision by casting the Nonlinear Complementarity Problem (NCP) of frictional contact into a Linear Complementarity Problem (LCP) to simplify computations. Moreover, such methods deploy non-smooth operations and cannot be automatically differentiated. In this paper, we propose (i) an extension of the staggered projections algorithm for more accurate solutions of the problem of contacts with friction. Based on this formulation, we introduce (ii) a differentiable simulator and an efficient way to compute the analytical derivatives of the involved optimization problems. Finally, (iii) we validate the proposed framework with a set of experiments to present a possible application of our differentiable simulator. In particular, using our approach we demonstrate accurate estimation of friction coefficients and object masses both in synthetic and real experiments.

The code of the differentiable solver is available at this link.

For more details, the paper is available on HAL and an introductory video containing a demo is available on Youtube:

The video of our ICRA presentation is also available:

You can cite this work with:

@ARTICLE{9363565,
  author={Le Lidec, Quentin and Kalevatykh, Igor and Laptev, Ivan and Schmid, Cordelia and Carpentier, Justin},
  journal={IEEE Robotics and Automation Letters}, 
  title={Differentiable Simulation for Physical System Identification}, 
  year={2021},
  volume={6},
  number={2},
  pages={3413-3420},
  doi={10.1109/LRA.2021.3062323}}